Introduction
The exam will be taken in August. After a period of thinking, trying to some write-ups should be helpful for retaking the exam. Goal: finishing Prolog on Wednesday (14th July 2021).
Body
Chapter 4
Chapter 4 has a variety of examples, it will be helpful if they are gone through.
1. Graph Introduction
The first example is an introduction to the graph. The goal is to:
- using the depth-first mechanism to find whether there is a path from a to e
- using the breadth-first mechanism to find whether there is a path from a to c
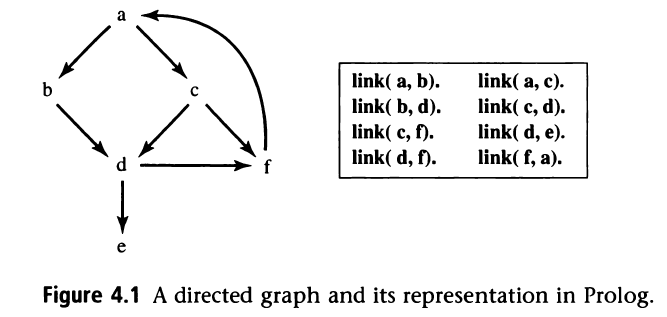
Program code is shown as below:
% database for graph
link(a,b).
link(a,c).
link(b,d).
link(c,d).
link(c,f).
link(d,e).
link(d,f).
link(f,a).
% using the depth-first mechanism to find whether there is a path from a to e
% base case
path(N1,N1).
% recursive case
path(N1,N3) :-
link(N1,N2),
path(N2,N3).
% using the breadth-first mechanism to find whether there is a path from a to c
% first, we need to transfer 'depth-first' to 'breadth-first' via conc(Path,_,_) or a new method list(Path)
% then, change path(N1,N2) to path(N1,N2,Path) for using our new method list(Path)
% new method list(Path)
list1([]).
list1([_|L]) :-
list1(L).
% improved path/3 for recording path
path(N1,N1,[N1]).
path(N1,N3,[N1|T]) :-
link(N1,N2),
path(N2,N3,T).
Question terminal is shown as below:
?- path(a,e).
true
?- path(a,c).
** Excution aborted **
?- list1(Path), path(a,c,Path).
Path = [a,c]
2. Robot Task Planning
The second example is trying to use the robot to clean the room:
- finding a way to represent the state of the robot, rubbish, basket
- determining the actions: pickup, drop, push(Pos1,Pos2), go(Pos1,Pos2)
- planning the time schedule and give the answer
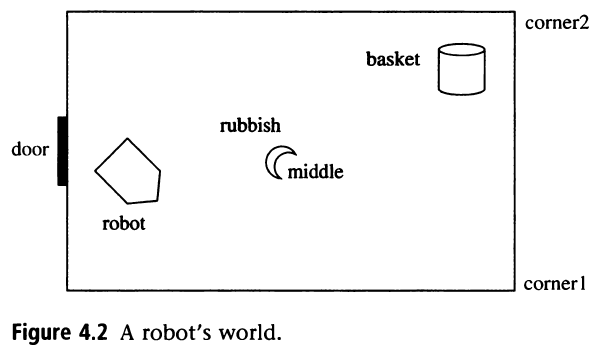
Program code is shown as below:
% first, the state will be represented by state(Pos1,Pos2,Pos3), saying that Pos1 is the position of the robot, Pos2 is the position of the basket, Pos3 is the position of the rubbish
% rubbish has its special state: floor(Pos1) is on the floor, held means it is carried by the robot, in_basket means it is in the basket
% second, actions will be represented as followed
% it is the idea from textbook, much simpler and clearer
% pickup, pick up rubbish from floor, more simpler
action1(state(Pos1,Pos2,floor(Pos1)),
pickup,
state(Pos1,Pos2,picked)).
% drop, drop rubbish into basket
action1(state(Pos1,Pos1,picked),
drop,
state(Pos1,Pos1,in_basket)).
% push(Pos1,Pos2), push basket from position Pos1 to Pos2
action1(state(Pos1,Pos1,Pos2),
push(Pos1,NewPos1),
state(NewPos1,NewPos1,Pos2)).
% go(Pos1,Pos2), go from Pos1 to Pos2
action1(state(Pos1,Pos2,Pos3),
go(Pos1,NewPos1),
state(NewPos1,Pos2,Pos3)).
% after determination of actions, plan/3 is also important for recording current state, goal state and schedules
% base case, for the end of the recursion
plan(GoalState,GoalState,[]).
% recursive case, for running the ai determination; otherwise, will not work
plan(CurrentState,GoalState, [Action|RPath]) :-
action1(CurrentState,Action,NewState),
plan(NewState,GoalState, RPath).
Question terminal is shown as below:
% Depth-first
?- plan(state(door,corner2,floor(middle)),state(_,_,in_basket),Plan).
Plan = [go(door, middle), pickup, go(middle, corner2), drop]
Plan = [go(door, middle), pickup, go(middle, corner2), drop, push(corner2, _1422)]
Plan = [go(door, middle), pickup, go(middle, corner2), drop, push(corner2, _1422), push(_1422, _1434)]
?- list1(Plan), plan(state(door,corner2,floor(middle)),state(_,_,in_basket),Plan).
Plan = [go(door, middle), pickup, go(middle, corner2), drop]
Plan = [go(door, corner2), push(corner2, middle), pickup, drop]
Plan = [go(door, middle), pickup, go(middle, corner2), drop, push(corner2, _1422)]
3. Trip planning
The third example is trying to try to plan a trip according to a sight-seeing plan and the timetable of boat transfers:
- building the database of timetable
- building some actions and helpers
- planning the time schedule and give the answer
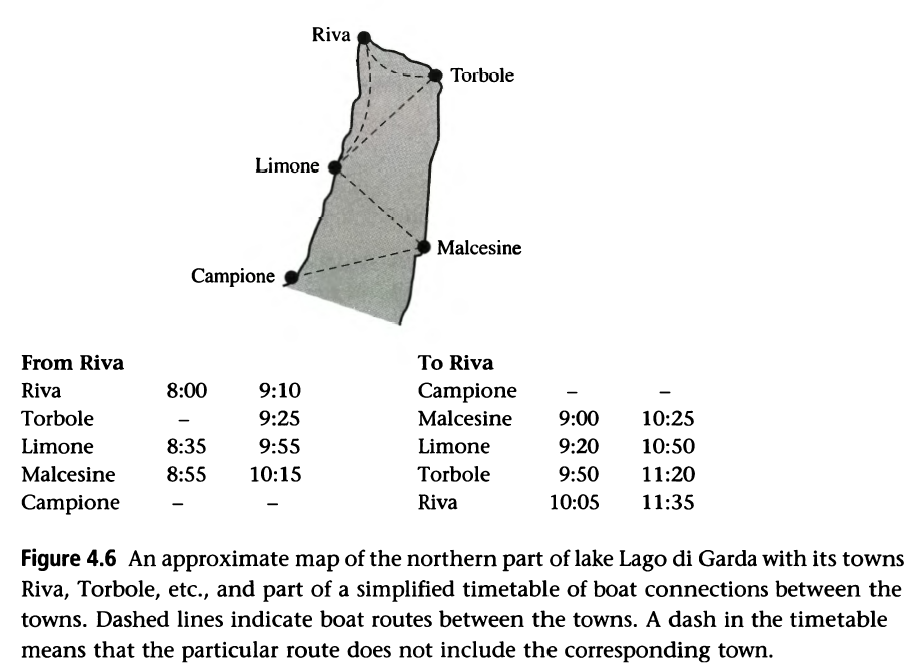
Program code is shown as below:
% define operators
:- op(200,xfx,and).
:- op(100,xfx, at).
:- op(50,xfx,:).
% database
timetable([riva at 8:00, limone at 8:35, malcesine at 8:55]).
timetable([riva at 9:10, torbole at 9:25, limone at 9:55, malcesine at 10:15]).
timetable([riva at 9:45, torbole at 10:00, limone at 10:30, malcesine at 10:50]).
timetable([riva at 11:45, torbole at 12:00, limone at 12:30, malcesine at 12:50]).
timetable([riva at 13:10, limone at 13:32, malcesine at 13:45]).
timetable([riva at 14:05, limone at 14:40, malcesine at 15:00]).
timetable([riva at 15:00, limone at 15:36, malcesine at 15:57, campione at 16:13]).
timetable([riva at 16:20, torbole at 16:35, limone at 17:05, malcesine at 17:25]).
timetable([riva at 18:05, torbole at 18:20, limone at 18:50, malcesine at 19:10]).
timetable([malcesine at 9:00, limone at 9:20, torbole at 9:50, riva at 10:05]).
timetable([malcesine at 10:25, limone at 10:50, torbole at 11:20, riva at 11:35]).
timetable([malcesine at 11:25, limone at 11:45, riva at 12:20]).
timetable([campione at 12:25, malcesine at 13:12, limone at 13:34, riva at 14:10]).
timetable([malcesine at 13:45, limone at 13:59, riva at 14:20]).
timetable([malcesine at 15:05, limone at 15:25, riva at 16:00]).
timetable([malcesine at 16:30, limone at 16:50, torbole at 17:20, riva at 17:35]).
timetable([malcesine at 18:15, limone at 18:35, torbole at 19:05, riva at 19:20]).
timetable([malcesine at 19:15, limone at 19:35, torbole at 20:05, riva at 20:20]).
% sublist, helper
% actually we can use member/2 since we only need 2 phases
sublist(S,L) :-
append(_,L2,L),
append(S,_,L2).
% breadth-first helper
list3([]).
list3([_|T]) :-
list3(T).
% sail/2, directly sail
sail(PlaceTime1, PlaceTime2) :-
timetable(Route),
sublist([PlaceTime1,PlaceTime2], Route).
% time difference
hour(H) :-
H >= 0,
H =< 24.
minute(MM) :-
MM >= 0,
MM =< 60.
time_diff(HH1:MM1, HH2:MM2, D) :-
hour(HH1),
hour(HH2),
minute(MM1),
minute(MM2),
D is (HH2-HH1)*60 + MM2-MM1.
% before/2
before(Time1,Time2) :-
time_diff(Time1,Time2,D),
D >= 0.
% textbook - idea
% main
% but still have problem of instantiation
schedule33(Current, Destination, Plan) :-
list3(Plan),
plan33(Current, Destination, Plan).
% base case
plan33(Destination, Destination, []).
% recursive case
plan33(Place at Time, Destination, [depart(Place,Time), arrive(NewPlace,NewTime)|Plan]) :-
sail(Place at Time, NewPlace at NewTime),
before(Time,NewTime),
plan33(NewPlace at NewTime, Destination, Plan).
plan33(Place at Time, Destination, [stay(Place,Time,NewTime)|Plan]) :-
sail(Place at NewTime, _),
before(Time,NewTime),
plan33(Place at NewTime, Destination, Plan).
% textbook - answer
% difference?
% but do not have problem of instantiation when using the same helpers, why???
schedule333(Start, Destination, [depart(Start),arrive(Next)|Rest]) :-
list3(Rest),
sail(Start,Next),
rest_schedule(Next,Destination,Rest).
rest_schedule(Place,Place,[]).
rest_schedule(CurrentPlace,Destination,[arrive(Next)|Rest]) :-
sail(CurrentPlace,Next),
rest_schedule(Next,Destination,Rest).
rest_schedule(Place at Time1, Destination,[stay(Place,Time1,Time2)|Rest]) :-
sail(Place at Time2,_),
before(Time1,Time2),
schedule(Place at Time2,Destination,Rest).
% Terminals Questions
% statistics(runtime,_), sail(riva at Start,_), before(17:00,Start),
% schedule333(riva at Start, riva at End, Plan), member(arrive(malcesine at _), Plan),
% statistics(runtime,[_,RunTime]).
Question terminal is shown as below:
?- schedule333(riva at 9:10,malcesine at FinalTime, Plan).
FinalTime = 10:15,
Plan = [depart riva at 9:10, arrive torbole at 9:25, arrive limone at 9:55, arrive malcesine at 10:15]
FinalTime = 15:57,
Plan = [depart riva at 9:10, arrive torbole at 9:25, arrive limone at 9:55, arrive malcesine at 10:15, stay(malcesine, 10:15, 15:57)]
...
?- schedule333(campione at Start, campione at End, Plan), member(stay(riva,T1,T2),Plan), time_diff(T1,T2,D), D>=45.
D = 50,
End = 16:13,
Plan = [depart campione at 12:25, arrive malcesine at 13:12, arrive limone at 13:34, arrive riva at 14:10, stay(riva, 14:10, 15:0), depart riva at 15:0 and arrive limone at 15:36, depart limone at 15:36 and arrive malcesine at 15:57, depart malcesine at 15:57 and arrive campione at 16:13],
Start = 12:25,
T1 = 14:10,
T2 = 15:0
4. Cryptarithmetic Problems
The fourth example is trying to solve a cryptarithmetic problems (as below), we can find that prolog is very easy to find an answer via AI/computer:
- building the database
- building some actions and helpers
- run
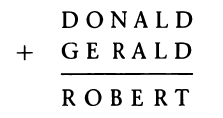
Program code is shown as below:
% primitive
cal1([X1,X2,X3,X4,X5,X6],[Y1,Y2,Y3,Y4,Y5,Y6],[Z1,Z2,Z3,Z4,Z5,Z6]) :-
X = X1*100000+X2*10000+X3*1000+X4*100+X5*10+X6,
Y = Y1*100000+Y2*10000+Y3*1000+Y4*100+Y5*10+Y6,
Z = Z1*100000+Z2*10000+Z3*1000+Z4*100+Z5*10+Z6,
Z =:= X + Y.
% improved
cal2(L1,L2,L3) :-
list_number(L1,N1),
list_number(L2,N2),
list_number(L3,N3),
N3 =:= N1 + N2.
% same digits
assign1([]).
assign1([H|T]) :-
% built-in predicate
select(H,[0,1,2,3,4,5,6,7,8,9],_),
assign1(T).
% cannot be same digits
assign2(_,[]).
assign2(L,[H|T]) :-
select(H,L,L1),
assign2(L1,T).
% transfering list to number
list_number(List,Number) :-
length(List,Length),
list_number_helper(List,Formula,Length),
Number is Formula.
% helper
list_number_helper([],0,_).
list_number_helper([H|T],F,P) :-
% 1. when giving number at outside, base case should be uninstantiated
% list_number_helper([1,3,2],F,3)
% list_number_helper([],0,_).
% here, **3** and **_**
% 2. when obtaining number at outside, base case should be instantiated
% here, **F** and **0**
P1 = P-1,
F = H*10**P1 + F1,
list_number_helper(T,F1,P1).
run(L1,L2,L3,Alphabets) :-
assign2([0,1,2,3,4,5,6,7,8,9],Alphabets),
cal2(L1,L2,L3).
From this exercise, we can knowing that:
- when giving number at outside, base case should be uninstantiated
- when obtaining number at outside, base case should be instantiated
Question terminal is shown as below:
?- run([D,O,N,A,L,D],[G,E,R,A,L,D],[R,O,B,E,R,T],[D,O,N,A,L,G,E,R,B,T]).
A = 4,
B = 3,
D = 5,
E = 9,
G = 1,
L = 8,
N = 6,
O = 2,
R = 7,
T = 0
Upadtes
- 于2021年7月14日1:37,完成对4.1-4.4的更新。
Acknowledgements
- Reference from the book Prolog Programming for Artificial Intelligence: Fourth Edition.
- Provided web system from SWISH: Sean's note for Prolog
Q.E.D.








