前言

写论文时候顺便写的
B站可能也会发个视频？
具体实现在：Github

正文

1. 概述

其实这篇博文主要讲的是Back-propagation (BP)，也就是反向传播算法，然后Excel写的二层神经网络只是用来作为介绍反向传播算法BP的一个例子罢了。

神经元模型感觉不用再赘述了，但是为了文章完整性这里还是放一个

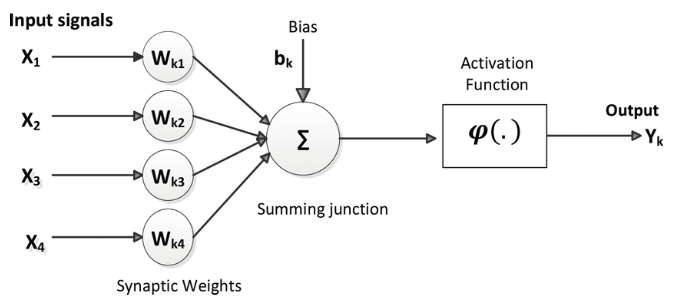
2-layers

然后是一个二层的神经网络，每层有2个神经元节点，最后为一个输出层，输出为[0/1]的category index。

接下来我们要引入我们的公式了：

公式分为2.1和2.2，其中2.1为Feed forward过程，而2.2主要阐述的是Back propagation的这一过程。具体的分别会在Section 2和 Section 3描述。

2. Feedforward propagation （正向传播过程）

正向传播过程字如其名，就是正向，从input输入到output输出的过程。

我们先由x1 和 x2 通过 weights (w_{1,1}, w_{1,2}, w_{2,1}, w_{2,2})算到了h1 和 h2
然后通过h1 和 h2 算到了最后的output 也就是y
这便是我们全部的正向传播过程。

3. Back-propagation （反向传播算法）

反向传播过程，也就是由output推向input的过程，其主要目的是为了通过改变weights，来将loss减到最小，所以很自然的，我们会想到通过求导来实现，求weights对loss的导数。由于loss 里面包含很多的weights，所以每个weights对loss自然求的是一个偏导数。其具体公式为：，其中eta为 learning rate，为学习速度，通常而言刚开始训练的时候学习速度会很大，然后会慢慢降低。（当然也会有schedule learning rate，取决于个人）

然后back propagation 其实也就是这个weights 从 output到input逐渐反推的过程罢了，至于为什么叫back propagation呢（我个人理解只是因为单纯和feedforward这个过程做个对比罢了，因为在我们把每一个w变化的偏导数算出来之后，会发现这东西算前一层weights的时候，根本没有需要后一层weights的任何东西，甚至可以跳过前面所有层的weights去算第一层的weights，唯一有影响的只是feedfoward时候的值x1、x2、h1、h2、y这类。）仅个人理解，未必正确！

然后我们可以把每个weights对loss的偏导求出来：

最后写到Excel里面就完事儿了！

4. Excel版二层神经网络

整个Excel版本其实很简单：

第1、2行为4个不变量，x1和x2分别为x在dimension1和dimension2的值，t为true value也就是真实值，eta为learning rate此处learning rate为常数。
第3行为weights的表头，然后为在当前weights下计算出来的h1、h2和y
从第4行开始，A列为第几次迭代，我们所有的input data 和label 都是相同的 [1,1] - 4也就是x1 = 1, x2 = 1, t = 4。

所以最后理所应当的，训练出来的神经网络 y会无限接近于4，也就是我们的真实值。可以看出来这里跟我本来预想的神经网络weights其实是很不一样的，我本来想的是可能会训练出一个什么 w_{1,1}=w_{1,2}=w_{2,1}=w_{2,2}=w_{3}=w_{4}这样一个东西出来，因为这样刚好[1,1]出来的结果就是4，结果这东西可能本来就与initial weights和learning rate有关。掉到了某一个local minimal里面，或者也许我的才送local minima（笑。）