前言

继上一篇，最近在玩Turing Complete，里面涉及了定点运算的左移右移，加减乘除。本来对这方面也不太熟悉，想了想，要不然就仔细做一篇博客算了。于是乎，上CSDN进行一顿搜，最后发现一片比较好的CSDN博文计算机组成原理定点运算-移位、加、减、乘、除（详细解析-看完就会），于是以这篇作为base来做。

正文

1. 移位运算

对于无符号的二进制移位与有符号的的二进制移位的差别就在于，无符号的最高位128跟着一起动，无符号的最高位128不变。

1.1 左移（无符号整数）

定义：数值的绝对值变为原来的2倍
实际操作：逻辑左移、低位添0、高位移丢
例子：

二进制	左移?位	十进制
01010011	0	83
10100110	1	166
01001100	2	76（高位丢失，否则就是256+76=332=2倍166）

P.S.: 此处是无符号数，所以最高位为128 而不是-128

1.2 右移（无符号整数）

定义：数值的绝对值变为原来的1/2倍
实际操作：逻辑右移、高位添0、低位移丢
例子：

二进制	右移?位	十进制
01010011	0	83
00101001	1	41（低位丢失，41约等于1/2倍83）
00010100	2	20（低位丢失，20约等于1/2倍41）

1.3 左移（符号整数）

定义：数值的绝对值变为原来的2倍
实际操作：逻辑左移、低位添0、高位移丢、但是符号位不变
例子：

二进制	左移?位	十进制
01010011	0	83
00100110	1	38（高位丢失，否则就是128+=166=2倍83）
01001100	2	76

1.4 右移（符号整数）

定义：数值的绝对值变为原来的1/2倍
实际操作：逻辑右移、高位添0、低位移丢、但是符号位不变
例子：

二进制	右移?位	十进制
01010011	0	83
00101001	1	41（低位丢失，41约等于1/2倍83）
00010100	2	20（低位丢失，20约等于1/2倍41）

2. 加法运算

2.1 算法

定义： A+B 就是平常的加法，这里我们仅考虑符号整数
实际操作：连同符号位一起相加，符号位产生的进位自然丢掉
例子1：A=11111101(-3), B=11111011(-5) ，求A+B=?

11111101
+11111011
——————
111111000 （符号位进位自然丢掉）

结果为11111000(-8)

例子2：A=00000111(7), B=11111011(-5) ，求A+B=?

00000111
+11111011
——————
100000010 （符号位进位自然丢掉）

结果为00000010(2)

2.2 溢出判断

但是请观察一下以下这个例子
例子3：A=10000001(-127), B=10000001(-127) ，求A+B=?

10000001
+10000001
——————
100000010 （符号位进位自然丢掉）

结果为00000010(2)。这一结果很明显，-127+(-127)怎么可能是-254呢，其实是因为我们省略掉了最高位，如果最高位是-256呢？那是不是很好理解了，就是那么我们的结果如果不省略掉最高位就变成了100000010 = -256+2=-254。这种因为我们只有8位而省略掉最高位导致结果不对的情况，我们称之为溢出。

如何判断溢出呢？我们将用异或运算来判断溢出，将符号位的进位与最高有效进位（注意是最高有效的进位，第七位的进位，而不是第七位的数值）进行异或运算，如果结果为1，则为溢出；如果结果为0，则无溢出。具体我们以例子1的结果和例子3的结果进行判断。

对于例子1的结果而言，111111000，符号位的最高位为被略去的1，最高有效位（第七位）为1，第七位的进位也为1，1 XOR 1 = 0，进行了异或运算之后结果为0，所以没有溢出。

对于例子2的结果而言，100000010，符号位的最高位为1，最高有效位（第七位）为0，最高有效位的进位为1，1 XOR 1 = 0，进行了异或运算之后结果为0，所以没有溢出。

对于例子3的结果而言，100000010，符号位的最高位为被略去的1，最高有效位（第七位）为0，但是第七位的进位也为0，1 XOR 0 = 1，进行了异或运算之后结果为1，所以因此判断此处发生溢出。

3. 减法运算

3.1 算法

定义：减法运算其实就是对减数进行一个neg取反的加法运算，A-B其实可以看为A+(-B)，这样一来，其实我们可以将减法视为多了一步（取反运算）的加法。
实际操作：对减数进行一个neg取反，然后将被减数与取反的减数进行加法运算
例子1：A=00000111(7), B=00000101(5) ，求A-B=?

首先对减数B进行neg取反，取反运算（对原码取补码，再补码的结果上+1）：

  00000101
neg
——————
  11111010
+00000001
——————
  11111011

得到结果11111011(-5)，然后对得到的结果(-B)和被减数A相加

00000111
+11111011
——————
100000010

结果为00000010，符号位进位为1，最高有效位为0，最高有效位的进位为1，1 XOR 1 = 0，没有溢出。

4. 乘法运算

定义：所谓乘法就是多少次相同的数，二进制的乘法可以与十进制的乘法进行类比，十进制中12×12=12×10+12×2；二进制也有一样的道理0b101×0b011 = 0b101×0b001+0b101×0b010。

十进制乘法的例子 12×12=144

    12
×12
——————
    12(×2)
  12(×1)
——————
    24
  12
——————
  144

同理，二进制乘法的例子 0b101×0b011=0b001111，此时我们暂时只考虑无符号整数，有符号整数需要对符号位进行异或运算来判断结果的正负性

      101
×  011
——————
      101(×1)
    101(×1)
  101(×0)
——————
      101
    101
  000
——————
001111

接下来介绍一下算法：被乘数按每个乘数所在位逐步左移，其数值是被乘数数值本身（乘数为1）还是0（乘数为0）由当前为乘数决定，最后四个部分的积分别相加。对于符号位的处理我们一般对符号位进行异或运算而获得。

5. 除法运算

定义：其实就是尽可能拼凑接近除数的值（说实话这部分有点忘记了，连十进制怎么做都差点忘记了，于是去看了一下Youtube的19 原码的除法运算，算是勉强想起来一点了，2333)

十进制除法的例子 1÷12=0.0833×12+0.0004

00833
——————
10
12 (10<12，只能上0)
——————
100
  96(12×8=96，可以上8)
——————
    40
    36(12×3=36，可以上3)
——————
      40
      36(12×3=36，可以上3)
——————
        4

最后的结果1÷12=0.0833 余0.0004

二进制除法的例子 0b1011÷0b1101，此时我们暂时只考虑无符号整数，有符号整数需要对符号位进行异或运算来判断结果的正负性

      01101
——————
1011
1101(1011小于1101，只能上0)
——————
10110
  1101(10110-1101=1101，可以上1)
——————
  11010
    1101(11010-1101=0101，可以上1)
——————
    1010
    1101(1010小于1101，只能上0)
——————
      10100
        1101(10100-1101=111，可以上1)
——————
          111

最后的结果0b1011÷0b1101=0b1101，余右移很多111（hhh，太懒了，不算了，有小可爱算出来了求帮忙评论回复一下是右移几个）（hmmm，最后还是找了下视频，最后的余数是00000111，也就是右移5位，如果没有错的话，:D）

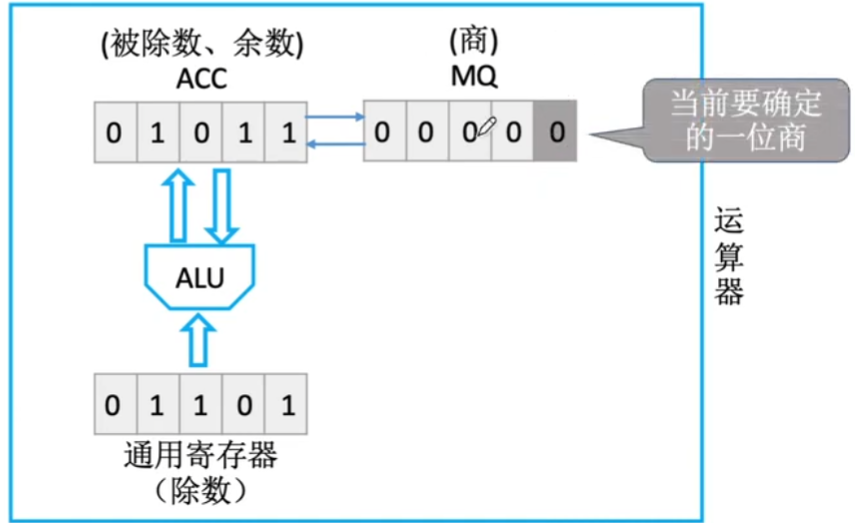
在介绍算法之前，看一下门电路图寄存器中的数值，算法如下，我们这里用的是恢复余数法：

默认上商1，那么就说明当前余数大于除数，所以余数-除数应该是正数
1. 如果符号位为1，说明应该上商0，将商变为0，ACC通过当前余数+除数，恢复成原来的余数，转到2
2. 如果符号位为0，说明上商1是正确的，保留商为1与ACC当前的余数，转到2
如果商MQ的位数已达到规定值，结束；否则ACC和MQ同时左移，转到1

P.S.:对于符号位的处理我们一般对符号位进行异或运算而获得。同时，余数的正负性与商相同。

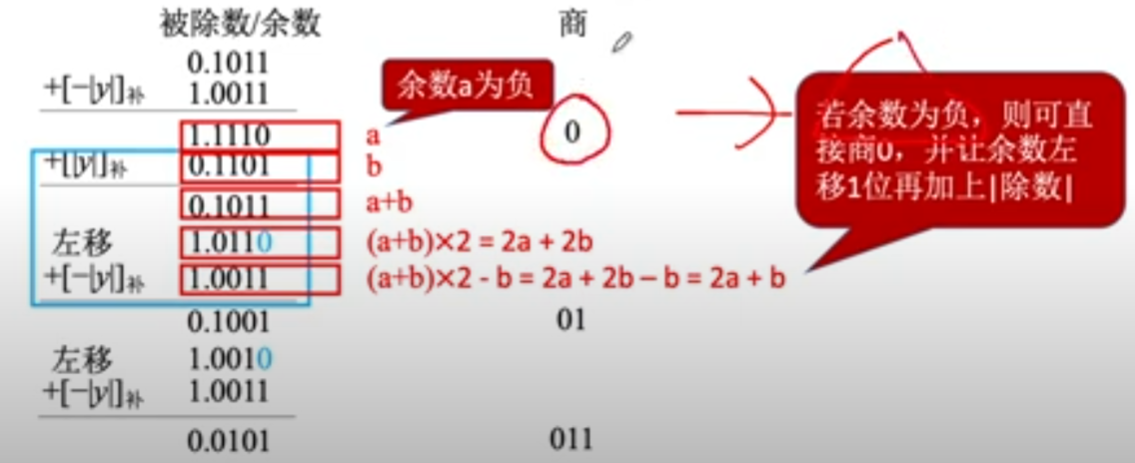
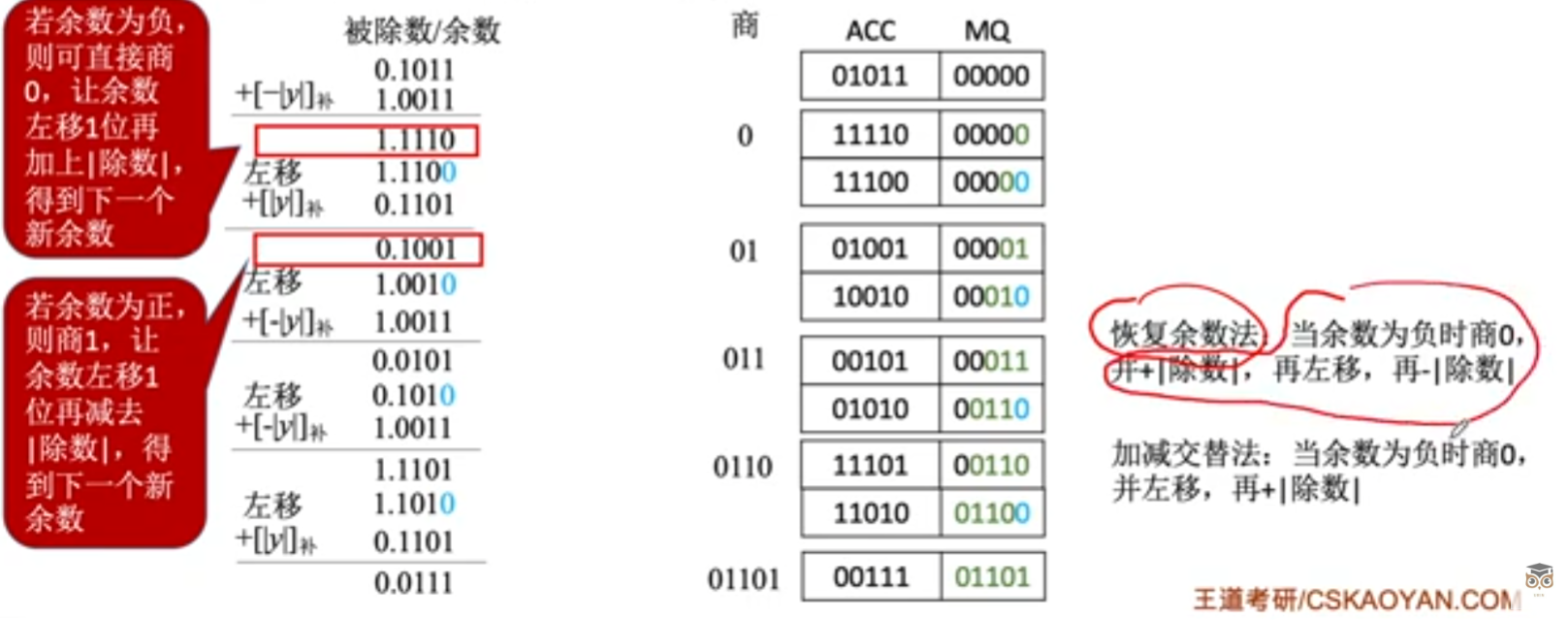
但是在介绍了恢复余数法之后，我们对这个过程进行分析（如上图），发现其实恢复余数的过程，其实就是先被除数c-除数a获得了余数b，若余数b的符号位为1说明其小于0，这时我们就要恢复余数，首先对b+a获得原来的被除数c(也就是b+a)，然后对其进行左移，左移的过程其实就是2×(b+a)，然后再减去除数b，获得余数2a+b。由此可知，我们其实可以不用做这么多复杂的恢复余数的过程，我们可以当余数b的符号位为1的时候，直接跳到新的余数2a+b进行判断，这便是不需要恢复余数的方法加减交替法。（具体寄存器ACC和MQ的值在下图）