这是一篇来自于旧站的重置文章。
最后这门课 Prolog部分 我得了(20/20),答疑的时候老师说我是 最优秀的几个答案之一(自豪挑眉状。)
Introduction
The exam will be taken in August. After a period of thinking, trying to some write-ups should be helpful for retaking the exam. Goal: finishing Prolog on Wednesday (14th July 2021).
Body
1. Chapter 4
Chapter 4 has a variety of examples, it will be helpful if they are gone through.
1.1 Graph Introduction
The first example is an introduction to the graph. The goal is to:
using the depth-first mechanism to find whether there is a path from a to e
using the breadth-first mechanism to find whether there is a path from a to c
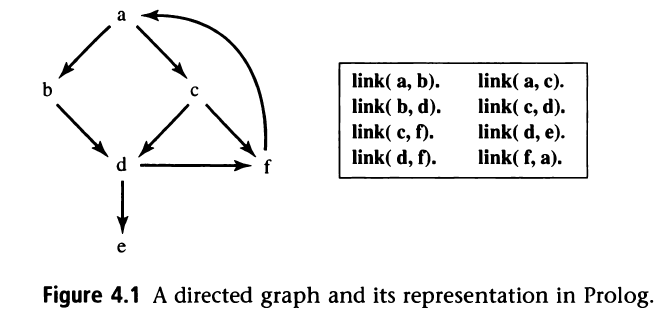
Program code is shown as below:
% database for graph
link(a,b).
link(a,c).
link(b,d).
link(c,d).
link(c,f).
link(d,e).
link(d,f).
link(f,a).
% using the depth-first mechanism to find whether there is a path from a to e
% base case
path(N1,N1).
% recursive case
path(N1,N3) :-
link(N1,N2),
path(N2,N3).
% using the breadth-first mechanism to find whether there is a path from a to c
% first, we need to transfer 'depth-first' to 'breadth-first' via conc(Path,_,_) or a new method list(Path)
% then, change path(N1,N2) to path(N1,N2,Path) for using our new method list(Path)
% new method list(Path)
list1([]).
list1([_|L]) :-
list1(L).
% improved path/3 for recording path
path(N1,N1,[N1]).
path(N1,N3,[N1|T]) :-
link(N1,N2),
path(N2,N3,T).Question terminal is shown as below:
?- path(a,e).
true
?- path(a,c).
** Excution aborted **
?- list1(Path), path(a,c,Path).
Path = [a,c]1.2 Robot Task Planning
The second example is trying to use the robot to clean the room:
finding a way to represent the state of the robot, rubbish, basket
determining the actions: pickup, drop, push(Pos1,Pos2), go(Pos1,Pos2)
planning the time schedule and give the answer
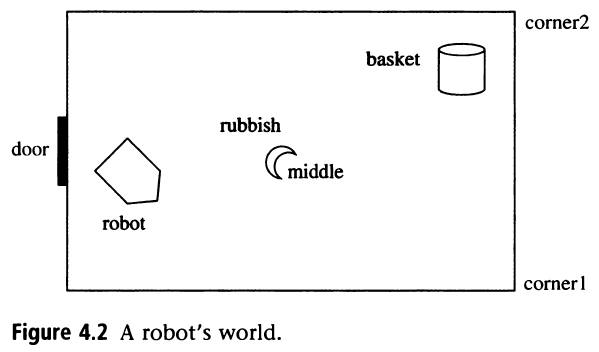
Program code is shown as below:
% first, the state will be represented by state(Pos1,Pos2,Pos3), saying that Pos1 is the position of the robot, Pos2 is the position of the basket, Pos3 is the position of the rubbish
% rubbish has its special state: floor(Pos1) is on the floor, held means it is carried by the robot, in_basket means it is in the basket
% second, actions will be represented as followed
% it is the idea from textbook, much simpler and clearer
% pickup, pick up rubbish from floor, more simpler
action1(state(Pos1,Pos2,floor(Pos1)),
pickup,
state(Pos1,Pos2,picked)).
% drop, drop rubbish into basket
action1(state(Pos1,Pos1,picked),
drop,
state(Pos1,Pos1,in_basket)).
% push(Pos1,Pos2), push basket from position Pos1 to Pos2
action1(state(Pos1,Pos1,Pos2),
push(Pos1,NewPos1),
state(NewPos1,NewPos1,Pos2)).
% go(Pos1,Pos2), go from Pos1 to Pos2
action1(state(Pos1,Pos2,Pos3),
go(Pos1,NewPos1),
state(NewPos1,Pos2,Pos3)).
% after determination of actions, plan/3 is also important for recording current state, goal state and schedules
% base case, for the end of the recursion
plan(GoalState,GoalState,[]).
% recursive case, for running the ai determination; otherwise, will not work
plan(CurrentState,GoalState, [Action|RPath]) :-
action1(CurrentState,Action,NewState),
plan(NewState,GoalState, RPath).Question terminal is shown as below:
% Depth-first
?- plan(state(door,corner2,floor(middle)),state(_,_,in_basket),Plan).
Plan = [go(door, middle), pickup, go(middle, corner2), drop]
Plan = [go(door, middle), pickup, go(middle, corner2), drop, push(corner2, _1422)]
Plan = [go(door, middle), pickup, go(middle, corner2), drop, push(corner2, _1422), push(_1422, _1434)]
?- list1(Plan), plan(state(door,corner2,floor(middle)),state(_,_,in_basket),Plan).
Plan = [go(door, middle), pickup, go(middle, corner2), drop]
Plan = [go(door, corner2), push(corner2, middle), pickup, drop]
Plan = [go(door, middle), pickup, go(middle, corner2), drop, push(corner2, _1422)]1.3 Trip planning
The third example is trying to try to plan a trip according to a sight-seeing plan and the timetable of boat transfers:
building the database of timetable
building some actions and helpers
planning the time schedule and give the answer
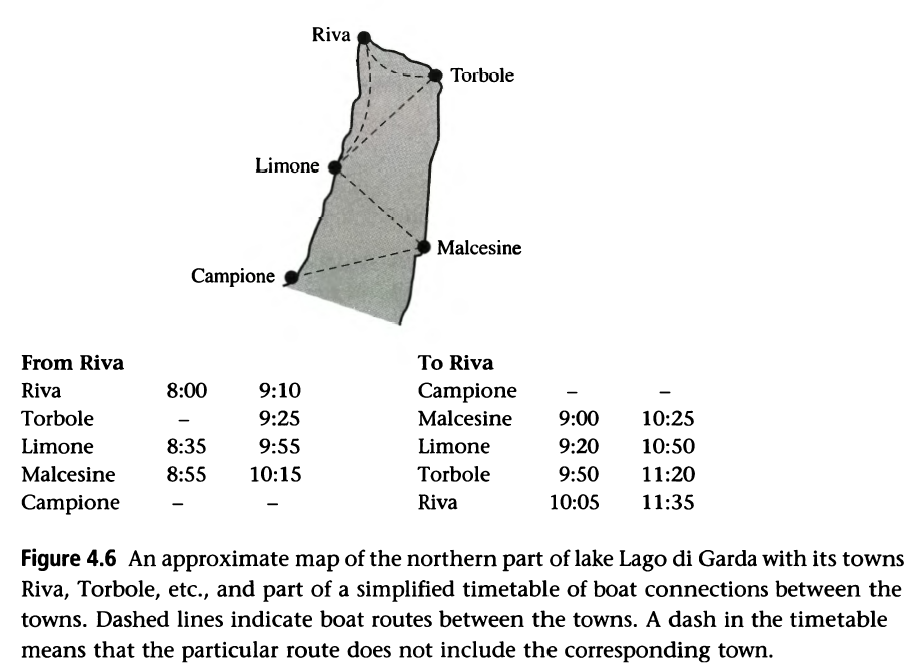
Program code is shown as below:
% define operators
:- op(200,xfx,and).
:- op(100,xfx, at).
:- op(50,xfx,:).
% database
timetable([riva at 8:00, limone at 8:35, malcesine at 8:55]).
timetable([riva at 9:10, torbole at 9:25, limone at 9:55, malcesine at 10:15]).
timetable([riva at 9:45, torbole at 10:00, limone at 10:30, malcesine at 10:50]).
timetable([riva at 11:45, torbole at 12:00, limone at 12:30, malcesine at 12:50]).
timetable([riva at 13:10, limone at 13:32, malcesine at 13:45]).
timetable([riva at 14:05, limone at 14:40, malcesine at 15:00]).
timetable([riva at 15:00, limone at 15:36, malcesine at 15:57, campione at 16:13]).
timetable([riva at 16:20, torbole at 16:35, limone at 17:05, malcesine at 17:25]).
timetable([riva at 18:05, torbole at 18:20, limone at 18:50, malcesine at 19:10]).
timetable([malcesine at 9:00, limone at 9:20, torbole at 9:50, riva at 10:05]).
timetable([malcesine at 10:25, limone at 10:50, torbole at 11:20, riva at 11:35]).
timetable([malcesine at 11:25, limone at 11:45, riva at 12:20]).
timetable([campione at 12:25, malcesine at 13:12, limone at 13:34, riva at 14:10]).
timetable([malcesine at 13:45, limone at 13:59, riva at 14:20]).
timetable([malcesine at 15:05, limone at 15:25, riva at 16:00]).
timetable([malcesine at 16:30, limone at 16:50, torbole at 17:20, riva at 17:35]).
timetable([malcesine at 18:15, limone at 18:35, torbole at 19:05, riva at 19:20]).
timetable([malcesine at 19:15, limone at 19:35, torbole at 20:05, riva at 20:20]).
% sublist, helper
% actually we can use member/2 since we only need 2 phases
sublist(S,L) :-
append(_,L2,L),
append(S,_,L2).
% breadth-first helper
list3([]).
list3([_|T]) :-
list3(T).
% sail/2, directly sail
sail(PlaceTime1, PlaceTime2) :-
timetable(Route),
sublist([PlaceTime1,PlaceTime2], Route).
% time difference
hour(H) :-
H >= 0,
H =< 24.
minute(MM) :-
MM >= 0,
MM =< 60.
time_diff(HH1:MM1, HH2:MM2, D) :-
hour(HH1),
hour(HH2),
minute(MM1),
minute(MM2),
D is (HH2-HH1)*60 + MM2-MM1.
% before/2
before(Time1,Time2) :-
time_diff(Time1,Time2,D),
D >= 0.
% textbook - idea
% main
% but still have problem of instantiation
schedule33(Current, Destination, Plan) :-
list3(Plan),
plan33(Current, Destination, Plan).
% base case
plan33(Destination, Destination, []).
% recursive case
plan33(Place at Time, Destination, [depart(Place,Time), arrive(NewPlace,NewTime)|Plan]) :-
sail(Place at Time, NewPlace at NewTime),
before(Time,NewTime),
plan33(NewPlace at NewTime, Destination, Plan).
plan33(Place at Time, Destination, [stay(Place,Time,NewTime)|Plan]) :-
sail(Place at NewTime, _),
before(Time,NewTime),
plan33(Place at NewTime, Destination, Plan).
% textbook - answer
% difference?
% but do not have problem of instantiation when using the same helpers, why???
schedule333(Start, Destination, [depart(Start),arrive(Next)|Rest]) :-
list3(Rest),
sail(Start,Next),
rest_schedule(Next,Destination,Rest).
rest_schedule(Place,Place,[]).
rest_schedule(CurrentPlace,Destination,[arrive(Next)|Rest]) :-
sail(CurrentPlace,Next),
rest_schedule(Next,Destination,Rest).
rest_schedule(Place at Time1, Destination,[stay(Place,Time1,Time2)|Rest]) :-
sail(Place at Time2,_),
before(Time1,Time2),
schedule(Place at Time2,Destination,Rest).
% Terminals Questions
% statistics(runtime,_), sail(riva at Start,_), before(17:00,Start),
% schedule333(riva at Start, riva at End, Plan), member(arrive(malcesine at _), Plan),
% statistics(runtime,[_,RunTime]).Question terminal is shown as below:
?- schedule333(riva at 9:10,malcesine at FinalTime, Plan).
FinalTime = 10:15,
Plan = [depart riva at 9:10, arrive torbole at 9:25, arrive limone at 9:55, arrive malcesine at 10:15]
FinalTime = 15:57,
Plan = [depart riva at 9:10, arrive torbole at 9:25, arrive limone at 9:55, arrive malcesine at 10:15, stay(malcesine, 10:15, 15:57)]
...
?- schedule333(campione at Start, campione at End, Plan), member(stay(riva,T1,T2),Plan), time_diff(T1,T2,D), D>=45.
D = 50,
End = 16:13,
Plan = [depart campione at 12:25, arrive malcesine at 13:12, arrive limone at 13:34, arrive riva at 14:10, stay(riva, 14:10, 15:0), depart riva at 15:0 and arrive limone at 15:36, depart limone at 15:36 and arrive malcesine at 15:57, depart malcesine at 15:57 and arrive campione at 16:13],
Start = 12:25,
T1 = 14:10,
T2 = 15:01.4 Cryptarithmetic Problems
The fourth example is trying to solve a cryptarithmetic problems (as below), we can find that prolog is very easy to find an answer via AI/computer:
building the database
building some actions and helpers
run
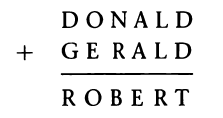
Program code is shown as below:
% primitive
cal1([X1,X2,X3,X4,X5,X6],[Y1,Y2,Y3,Y4,Y5,Y6],[Z1,Z2,Z3,Z4,Z5,Z6]) :-
X = X1*100000+X2*10000+X3*1000+X4*100+X5*10+X6,
Y = Y1*100000+Y2*10000+Y3*1000+Y4*100+Y5*10+Y6,
Z = Z1*100000+Z2*10000+Z3*1000+Z4*100+Z5*10+Z6,
Z =:= X + Y.
% improved
cal2(L1,L2,L3) :-
list_number(L1,N1),
list_number(L2,N2),
list_number(L3,N3),
N3 =:= N1 + N2.
% same digits
assign1([]).
assign1([H|T]) :-
% built-in predicate
select(H,[0,1,2,3,4,5,6,7,8,9],_),
assign1(T).
% cannot be same digits
assign2(_,[]).
assign2(L,[H|T]) :-
select(H,L,L1),
assign2(L1,T).
% transfering list to number
list_number(List,Number) :-
length(List,Length),
list_number_helper(List,Formula,Length),
Number is Formula.
% helper
list_number_helper([],0,_).
list_number_helper([H|T],F,P) :-
% 1. when giving number at outside, base case should be uninstantiated
% list_number_helper([1,3,2],F,3)
% list_number_helper([],0,_).
% here, **3** and **_**
% 2. when obtaining number at outside, base case should be instantiated
% here, **F** and **0**
P1 = P-1,
F = H*10**P1 + F1,
list_number_helper(T,F1,P1).
run(L1,L2,L3,Alphabets) :-
assign2([0,1,2,3,4,5,6,7,8,9],Alphabets),
cal2(L1,L2,L3).From this exercise, we can knowing that:
when giving number at outside, base case should be uninstantiated
when obtaining number at outside, base case should be instantiated
Question terminal is shown as below:
?- run([D,O,N,A,L,D],[G,E,R,A,L,D],[R,O,B,E,R,T],[D,O,N,A,L,G,E,R,B,T]).
A = 4,
B = 3,
D = 5,
E = 9,
G = 1,
L = 8,
N = 6,
O = 2,
R = 7,
T = 02. Back-up
虽然当时没有继续写下去了,但是我感觉我当时的Prolog代码真的写的太挺不错的,留一下档案,万一以后要用呢。
2.1 Chapter 4 Programming Examples
% database
link(a,b).
link(a,c).
link(b,d).
link(c,d).
link(c,f).
link(d,e).
link(d,f).
link(f,a).
% path
path(N1,N1).
path(N1,N3) :-
link(N1,N2),
path(N2,N3).
% recording the path
path(N1,N1,[N1]).
path(N1,N3,[N1|T]) :-
link(N1,N2),
path(N2,N3,T).
% length
length1([],0).
length1([_|T],X) :-
length1(T,X1),
X is X1 + 1.
% concat
concat1([],L,L).
concat1([H|T],L,[H|T1]) :-
concat1(T,L,T1).
% list
list1([]).
list1([_|L]) :-
list1(L).
% Using breadth-first to find path(a,c,Path)
% e.g., concat1(Path,_,_), path(a,c,Path).
% e.g., list(Path), path(a,c,Path)
% otherwise, we cannot find path(a,c,Path), because it is a depth-first infinite loop
% ch 4.2
/* Sean's first attempt
on(door).
on(corner2).
on(cornor2).
on(middle).
busy(held).
run(position(robot,Pos1), position(basket,Pos2), position(rubbish,middle), Path) :-
action(position(robot,Pos1), position(basket,Pos2), position(rubbish,middle), Path).
action(position(robot,Pos1), position(basket,Pos2), position(rubbish,Pos3),[go(Pos1,Pos3)|T]) :-
on(Pos3),
Pos1 \= Pos3,
Pos3 \= held,
action(position(robot,Pos3), position(basket,Pos2), position(rubbish,Pos3),T).
action(position(robot,Pos3), position(basket,Pos2), position(rubbish,Pos3),[pick(robot,Pos3)|T]) :-
Pos3 \= held,
action(position(robot,Pos3), position(basket,Pos2), position(rubbish,held),T).
action(position(robot,Pos3), position(basket,Pos2), position(rubbish,held),[go(Pos3,Pos2)|T]) :-
Pos3 \= Pos2,
action(position(robot,Pos2), position(basket,Pos2), position(rubbish,held),T).
action(position(robot,Pos2), position(basket,Pos2), position(rubbish,held),[drop(robot,Pos2)|T]) :-
action(position(robot,Pos2), position(basket,Pos2), position(rubbish,in_basket),T).
action(position(robot,Pos2), position(basket,Pos2), position(rubbish,in_basket),[]).
*/
run(state(Ro1,Ba1,Ru1), state(Ro2,Ba2,Ru2), Path) :-
action(state(Ro1,Ba1,Ru1), state(Ro2,Ba2,Ru2), Path).
% remember the []
action(state(Ro1,Ba1,Ru1),state(Ro1,Ba1,Ru1), []).
% pickup, pick up rubbish from floor
action(state(Ro1,Ba1,floor(Ro1)), state(Ro2,Ba2,Ru2), [pickup(Ro1) |RPath]) :-
action(state(Ro1,Ba1,pick), state(Ro2,Ba2,Ru2), RPath).
% drop, drop rubbish into basket
action(state(Ba1,Ba1,pick),state(Ro2,Ba2,Ru2), [drop(Ba1)|RPath]) :-
action(state(Ba1,Ba1,in_basket),state(Ro2,Ba2,Ru2), RPath).
% push(Pos1,Pos2), push basket from position Pos1 to Pos2
action(state(Ba1,Ba1,Ru1),state(Ro2,Ba2,Ru2), [push(Ba1,PushedBa1)|RPath]) :-
action(state(PushedBa1,PushedBa1,Ru1),state(Ro2,Ba2,Ru2), RPath).
% go(Pos1,Pos2), go from Pos1 to Pos2
action(state(Ro1,Ba1,Ru1), state(Ro2,Ba2,Ru2), [go(Ro1,WentRo1) |RPath]) :-
action(state(WentRo1,Ba1,Ru1), state(Ro2,Ba2,Ru2), RPath).
% textbook - idea
% pickup, pick up rubbish from floor, more simpler
action1(state(Pos1,Pos2,floor(Pos1)),
pickup,
state(Pos1,Pos2,picked)).
% drop, drop rubbish into basket
action1(state(Pos1,Pos1,picked),
drop,
state(Pos1,Pos1,in_basket)).
% push(Pos1,Pos2), push basket from position Pos1 to Pos2
action1(state(Pos1,Pos1,Pos2),
push(Pos1,NewPos1),
state(NewPos1,NewPos1,Pos2)).
% go(Pos1,Pos2), go from Pos1 to Pos2
action1(state(Pos1,Pos2,Pos3),
go(Pos1,NewPos1),
state(NewPos1,Pos2,Pos3)).
plan(GoalState,GoalState,[]).
plan(CurrentState,GoalState, [Action|RPath]) :-
action1(CurrentState,Action,NewState),
plan(NewState,GoalState, RPath).
% ch 4.3 Trip planning
% define operators
:- op(200,xfx,and).
:- op(150,fx, depart).
:- op(150,fx, arrive).
:- op(100,xfx, at).
:- op(50,xfx,:).
% database
timetable([riva at 8:00, limone at 8:35, malcesine at 8:55]).
timetable([riva at 9:10, torbole at 9:25, limone at 9:55, malcesine at 10:15]).
timetable([riva at 9:45, torbole at 10:00, limone at 10:30, malcesine at 10:50]).
timetable([riva at 11:45, torbole at 12:00, limone at 12:30, malcesine at 12:50]).
timetable([riva at 13:10, limone at 13:32, malcesine at 13:45]).
timetable([riva at 14:05, limone at 14:40, malcesine at 15:00]).
timetable([riva at 15:00, limone at 15:36, malcesine at 15:57, campione at 16:13]).
timetable([riva at 16:20, torbole at 16:35, limone at 17:05, malcesine at 17:25]).
timetable([riva at 18:05, torbole at 18:20, limone at 18:50, malcesine at 19:10]).
timetable([malcesine at 9:00, limone at 9:20, torbole at 9:50, riva at 10:05]).
timetable([malcesine at 10:25, limone at 10:50, torbole at 11:20, riva at 11:35]).
timetable([malcesine at 11:25, limone at 11:45, riva at 12:20]).
timetable([campione at 12:25, malcesine at 13:12, limone at 13:34, riva at 14:10]).
timetable([malcesine at 13:45, limone at 13:59, riva at 14:20]).
timetable([malcesine at 15:05, limone at 15:25, riva at 16:00]).
timetable([malcesine at 16:30, limone at 16:50, torbole at 17:20, riva at 17:35]).
timetable([malcesine at 18:15, limone at 18:35, torbole at 19:05, riva at 19:20]).
timetable([malcesine at 19:15, limone at 19:35, torbole at 20:05, riva at 20:20]).
% sublist, helper
sublist(S,L) :-
append(_,L2,L),
append(S,_,L2).
% breadth-first helper
list3([]).
list3([_|T]) :-
list3(T).
% sail/2, directly sail
sail(PlaceTime1, PlaceTime2) :-
timetable(Route),
sublist([PlaceTime1,PlaceTime2], Route).
% time difference
hour(H) :-
H >= 0,
H =< 24.
minute(MM) :-
MM >= 0,
MM =< 60.
time_diff(HH1:MM1, HH2:MM2, D) :-
hour(HH1),
hour(HH2),
minute(MM1),
minute(MM2),
D is (HH2-HH1)*60 + MM2-MM1.
% before/2
before(Time1,Time2) :-
time_diff(Time1,Time2,D),
D >= 0.
% main method for running
schedule(PlaceTime1, PlaceTime2, Plan) :-
list3(Plan),
plan3(PlaceTime1, PlaceTime2, Plan).
% plan
% base case
plan3(DestinationTime, DestinationTime, []).
% recursive case
plan3(Place1 at Time1, DestinationTime, [depart Place1 at Time1 and arrive Place2 at Time2|Plan]) :-
sail(Place1 at RTime1, Place2 at Time2),
before(Time1,RTime1),
plan3(Place2 at Time2, DestinationTime, Plan).
% textbook - idea
% main
schedule33(Current, Destination, Plan) :-
list3(Plan),
plan33(Current, Destination, Plan).
% base case
plan33(Destination, Destination, []).
% recursive case
plan33(Place at Time, Destination, [depart(Place,Time), arrive(NewPlace,NewTime)|Plan]) :-
sail(Place at Time, NewPlace at NewTime),
before(Time,NewTime),
plan33(NewPlace at NewTime, Destination, Plan).
plan33(Place at Time, Destination, [stay(Place,Time,NewTime)|Plan]) :-
sail(Place at NewTime, _),
before(Time,NewTime),
plan33(Place at NewTime, Destination, Plan).
% textbook - answer
% differece?
schedule333(Start, Destination, [depart(Start),arrive(Next)|Rest]) :-
list3(Rest),
sail(Start,Next),
rest_schedule(Next,Destination,Rest).
rest_schedule(Place,Place,[]).
rest_schedule(CurrentPlace,Destination,[arrive(Next)|Rest]) :-
sail(CurrentPlace,Next),
rest_schedule(Next,Destination,Rest).
rest_schedule(Place at Time1, Destination,[stay(Place,Time1,Time2)|Rest]) :-
sail(Place at Time2,_),
before(Time1,Time2),
schedule(Place at Time2,Destination,Rest).
% Terminals Questions
% statistics(runtime,_), sail(riva at Start,_), before(17:00,Start),
% schedule333(riva at Start, riva at End, Plan), member(arrive(malcesine at _), Plan),
% statistics(runtime,[_,RunTime]).
% ch 4.4
% shorter codes, stronger functions
cal1([X1,X2,X3,X4,X5,X6],[Y1,Y2,Y3,Y4,Y5,Y6],[Z1,Z2,Z3,Z4,Z5,Z6]) :-
X = X1*100000+X2*10000+X3*1000+X4*100+X5*10+X6,
Y = Y1*100000+Y2*10000+Y3*1000+Y4*100+Y5*10+Y6,
Z = Z1*100000+Z2*10000+Z3*1000+Z4*100+Z5*10+Z6,
Z =:= X + Y.
cal2(L1,L2,L3) :-
list_number(L1,N1),
list_number(L2,N2),
list_number(L3,N3),
N3 =:= N1 + N2.
% same digits
assign1([]).
assign1([H|T]) :-
% built-in predicate
select(H,[0,1,2,3,4,5,6,7,8,9],_),
assign1(T).
% cannot be same digits
assign2(_,[]).
assign2(L,[H|T]) :-
select(H,L,L1),
assign2(L1,T).
% transfering list to number
list_number(List,Number) :-
length(List,Length),
list_number_helper(List,Formula,Length),
Number is Formula.
% helper
list_number_helper([],0,_).
list_number_helper([H|T],F,P) :-
% 1. when giving number at outside, base case should be uninstantiated
% list_number_helper([1,3,2],F,3)
% list_number_helper([],0,_).
% here, **3** and **_**
% 2. when obtaining number at outside, base case should be instantiated
% here, **F** and **0**
P1 = P-1,
F = H*10**P1 + F1,
list_number_helper(T,F1,P1).
run(L1,L2,L3,Alphabets) :-
assign2([0,1,2,3,4,5,6,7,8,9],Alphabets),
cal2(L1,L2,L3).2.2 Chapter 5 Controlling Backtracking
% ch 5.1
% detect concentration of the pollutant and alert
f(X,normal) :-
0 < X,
X =< 3, !.
f(X,alert1) :-
X < 6, !.
f(X,alert2) :-
X >= 6.
% ch 5.2
% max/3 using cut '!'
max(X,Y,X) :-
X > Y, !.
max(_,Y,Y).
% member1/2
member1(X,L) :-
append(_,[X|_],L).
% member2/2 using cut '!'
% '!' after append, will not go back to append,
% since no false meet, and not alternative after '!'
member2(X,L) :-
append(_,[X|_],L),!.
% add/3 using cut '!'
add(X,L,L) :- member1(X,L), !.
add(X,L,[X|L]).
% competition
% database
beat(tom,jim).
beat(ann,tom).
beat(pat,jim).
% iterate all, member(P,[tom,ann,jim,pat]), class(P,C).
class(P,fighter) :-
beat(P,_),
beat(_,P), !.
class(P,sportsman) :-
beat(_,P), !.
class(_,winner).
% ex 5.1
p(1).
p(2) :- !.
p(3).
/*
* ?- p(X).
* X = 1.
* X = 2.
*
* ?- p(X),p(Y)
* X = 1, Y = 1.
* X = 1, Y = 2.
* X = 2, Y = 1.
* X = 2, Y = 2.
*
* ?- p(X), !, p(Y).
* X = 1, Y = 1.
* X = 1, Y = 2.
*/
% ex 5.2
class1(N,positive) :-
N > 0, !.
class1(N,negative) :-
N < 0, !.
class1(0,zero).
% ex 5.3
% without cut
split([],[],[]).
split([H|L],[H|P],N) :-
class1(H,positive),
split(L,P,N)
;
class1(H,zero),
split(L,P,N).
split([H|L],P,[H|N]) :-
class1(H,negative),
split(L,P,N).
% with cut
% empty list
split1([],[],[]).
split1([H|L],P,[H|N]) :-
class1(H,negative),
split1(L,P,N), !.
% at least no empty list
split1([H|L],[H|P],N) :-
split1(L,P,N).
% ch 5.3
% after '!', all cannot backtrack to before '!'
different(X,X) :- !, fail.
different(_,_).
% more compact, true - true, fail - false
different1(X,Y) :-
X = Y, !, fail
;
true.
% using '\+' as 'not'
different2(X,Y) :-
\+ X = Y.
% ex 5.4
% in C, not in R
findout([],_,[]) :- !.
findout([H|C],R,[H|L]) :-
\+ member(H,R),
findout(C,R,L), !.
findout([_|C],R,L) :-
findout(C,R,L).
% ex 5.5
set_difference(S1,S2,D) :-
findout(S1,S2,D).
% ex 5.6
% without using not
unifiable1([],_,[]) :- !.
unifiable1([H1|T],H2,L) :-
H1 \= H2, % not(H1 = H2)
unifiable1(T,H2,L), !.
unifiable1([H1|T],H2,[H1|L]) :-
unifiable1(T,H2,L).
% using not
% when using not => making true become fail, making fail become true
% amazing
unifiable2([],_,[]) :- !.
unifiable2([H1|T],H2,L) :-
\+ H1 = H2,
unifiable2(T,H2,L).
unifiable2([H1|T],H2,[H1|L]) :-
\+ H1 \= H2,
unifiable2(T,H2,L).
% third methods
unifiable3([], _, []).
unifiable3([H|T], Term, L) :- % Remember this model/ condition
not(H = Term),
% In this case, this ! only cut this layer/ level
% When goes to next unifiable1, this ! will not affect that level
unifiable3(T, Term, L), !. % Remember first put '!' in easier place.
unifiable3([H|T], Term, [H|L]) :- % Remember this model/ condition
unifiable3(T, Term, L).
% ch 5.42.3 Chapter 6 Built-in Predicates
% ch 6.1
% without ordering
count1_helper(_,[],0).
count1_helper(A,[B|L],N) :-
atom(B),
A = B,
N = N1 + 1,
count1_helper(A,L,N1), !
;
count1_helper(A,L,N).
count1(A,L,N) :-
count1_helper(A,L,Formula),
N is Formula.
% need order to make "is"
count2(_,[],0).
count2(A,[B|L],N) :-
% without this, rejects all others alertnatives
atom(B),
A = B,
count2(A,L,N1),
% N1 should after count2, when get the answer
N is N1 + 1, !
;
count2(A,L,N).
% sum
sum(L1,L2,L3,Digs) :-
derive_list(L1,Digs,Digs1),
derive_list(L2,Digs1,Digs2),
derive_list(L3,Digs2,_),
add_zero(L1,L2,L3,NL1,NL2,NL3),
sum_helper(NL1,NL2,NL3,0,_).
last([H|T],RH1,T1) :-
reverse([H|T],[RH1|RT1]),
reverse(RT1,T1).
sum_helper([],[],[],0,0) :- !.
sum_helper(L1,L2,L3,B,F) :-
last(L1,SH1,SL1),
last(L2,SH2,SL2),
last(L3,SH3,SL3),
SH3 is ((SH1+SH2+B) mod 10),
F is ((SH1+SH2+B) // 10),
sum_helper(SL1,SL2,SL3,F,_).
derive(X,Digs,Digs1) :-
append(A,[X|B],Digs),
append(A,B,Digs1).
% write twice time, less use "!", dangerous
derive_list([],Rest,Rest).
derive_list([H|T],Digs,Rest) :-
var(H),
derive(H,Digs,Digs1),
derive_list(T,Digs1,Rest)
;
nonvar(H),
derive_list(T,Digs,Rest).
% add zero for the list not equal to the maximum list
add_zero(L1,L2,L3,NL1,NL2,NL3) :-
reverse(L1,RL1),
reverse(L2,RL2),
reverse(L3,RL3),
add_zero_helper(RL1,RL2,RL3,RNL1,RNL2,RNL3),
reverse(RNL1,NL1),
reverse(RNL2,NL2),
reverse(RNL3,NL3).
add_zero_helper([],[],[],[],[],[]) :- !.
add_zero_helper([],[H2|T2],[H3|T3],[0|NT1],[H2|NT2],[H3|NT3]) :-
add_zero_helper([],T2,T3,NT1,NT2,NT3), !.
add_zero_helper([H1|T1],[],[H3|T3],[H1|NT1],[0|NT2],[H3|NT3]) :-
add_zero_helper(T1,[],T3,NT1,NT2,NT3), !.
add_zero_helper([H1|T1],[H2|T2],[],[H1|NT1],[H2|NT2],[0|NT3]) :-
add_zero_helper(T1,T2,[],NT1,NT2,NT3), !.
add_zero_helper([],[],[H3|T3],[0|NT1],[0|NT2],[H3|NT3]) :-
add_zero_helper([],[],T3,NT1,NT2,NT3), !.
add_zero_helper([],[H2|T2],[],[0|NT1],[H2|NT2],[0|NT3]) :-
add_zero_helper([],T2,[],NT1,NT2,NT3), !.
add_zero_helper([H1|T1],[],[],[H1|NT1],[0|NT2],[0|NT3]) :-
add_zero_helper(T1,[],[],NT1,NT2,NT3), !.
add_zero_helper([H1|T1],[H2|T2],[H3|T3],[H1|NT1],[H2|NT2],[H3|NT3]) :-
add_zero_helper(T1,T2,T3,NT1,NT2,NT3), !.
% ex 6.1
% incomplete
simplify_class(X,[],[X]) :-
atom(X), !.
simplify_class(X,[X],[]) :-
number(X), !.
simplify_class(X+Y,N,A) :-
simplify_class(X,N1,A1),
simplify_class(Y,N2,A2),
append(N1,N2,N),
append(A1,A2,A),!.
sum_list([],0).
sum_list([H|T],X) :-
sum_list(T,X1),
X is X1 + H.
list_show([X],X) :- !.
list_show([H|T],X) :-
list_show(T,X1),
X = H + X1.
simplify(L,E) :-
simplify_class(L,N,A),
sum_list(N,LN),
list_show(A,LA),
E = LN + LA.
% ex 6.2
add_to_tail(X,[H|T],[X,H|T]) :-
var(H), !.
add_to_tail(X,[H|T],[H|T1]) :-
nonvar(H),
addToTail_helper(X,T,T1),!.
% ch 6.2
% by Sean ownself
multiply_list(_,[],[]).
multiply_list(F,[H|T],[H1|T1]) :-
H1 is F * H,
multiply_list(F,T,T1).
enlarge(Fig, Factor, Fig1) :-
Fig =.. [Type|Val],
multiply_list(Factor,Val,Val1),
Fig1 =.. [Type|Val1].
substitute_list(_,[],_,[]).
substitute_list(T,[L|LTail],T1,[L1|LTail1]) :-
substitute(T,L,T1,L1),
substitute_list(T,LTail,T1,LTail1).
substitute(T,T,T1,T1) :- !.
substitute(T,L,T1,L1) :-
L =.. [Name|Remain],
substitute_list(T,Remain,T1,Remain1),
L1 =.. [Name|Remain1].
eval1_list(Exp,[],Exp).
eval1_list(Exp,[Symbol=Value|T],Exp2) :-
substitute(Symbol,Exp,Value,Exp1),
eval1_list(Exp1,T,Exp2).
eval1(Exp,SymbolValues,Val) :-
eval1_list(Exp,SymbolValues,Exp1),
Val is Exp1.
% ex 6.3
ground1(Term) :-
Term =.. [_|Args],
noVar(Args).
noVar([]) :- !.
noVar([H|_]) :-
var(H),!, fail.
noVar([H|T]) :-
nonvar(H),
noVar(T).
% ex 6.4
% recursive method
not_compound(A,B) :-
\+ compound(A),
\+ compound(B).
% not all A and B are not compound
subsumes(A,B) :-
not_compound(A,B),
var(A),
nonvar(B),
!, true
;
not_compound(A,B),
nonvar(A),
nonvar(B),
!, fail
;
not_compound(A,B),
var(A),
var(B),
!, fail
;
not_compound(A,B),
nonvar(A),
var(B),
!, fail
;
compound(A),
\+ compound(B),
!, true
;
\+ compound(A),
compound(B),
!, fail.
% all A and B are compound
subsumes(A,B) :-
arg(1,A,A1),
arg(1,B,B1),
subsumes(A1,B1).
% ch 6.4
multiply_table(X,Y,Z,L) :-
member(X,L),
member(Y,L),
Z is X*Y,
assert(multiply1(X,Y,Z)).
% ch 6.5
max1(X,Y,Z) :-
X >= Y -> Z = X ; Z = Y.
dosquare :-
repeat,
read(X),
( \+ number(X), !
;
Y is X*X,
write(Y)
% using "fail" here, do not need to wait true again.
).
% ch 6.6
age(peter,7).
age(ann,5).
age(pat,8).
age(tom,5).
% bagof(Output,Formula,Outputs)
% e.g. 1, only Name of children
% bagof(X,age(X,Y),List).
% List = [ann, tom], Y = 5
% List = [peter], Y = 7
% List = [pat], Y = 8
%
% e.g. 2, whole age compound/structure
% it collects all variables in the 2nd argument,
% and outputs as the form of 1st argument
% bagof(X/Y,age(X,Y),List).
% List = [peter/7, ann/5, pat/8, tom/5]
%
% e.g. 3, duplicate
% bagof(Age,Child^age(Child,Age),List).
% List = [7, 5, 8, 5]
% bagof: duplicate, non-ordered list
% setof: no duplicate, ordered set
% findall: duplicate, non-ordered list, but without "Age^", it only outputs the data in 1st argument
% ex 6.8
% previous, without bagof/3
% powerset([],[]).
% powerset([H|T],[H1|T1]) :-
% H1 is H*H,
% powerset(T,T1).
% now, with bagof/3
% duplicate
% ?- powerset([1,2,3],L).
% L = [[], [1], [1, 2], [1, 2, 3], [], [2], [2, 3], [], [3], []]
powerset(L,L1) :-
bagof(X,powerset_helper(L,X),L1).
% using setof/3
% non-duplicate
% ?- powerset1([1,2,3],L).
% L = [[], [1], [1, 2], [1, 2, 3], [2], [2, 3], [3]]
powerset1(L,L1) :-
setof(X,powerset_helper(L,X),L1).
powerset_helper(L,X) :-
append(_,L2,L),
append(X,_,L2).
% ex 6.9
% is this correct?
copy_term1(Term,Copy) :-
bagof(X,member(X,Term),Copy).
% ch 6.7
% interaction between program and user
cube(N,C) :-
C is N**3.
% Can directly use write('Next item, please:')
input_format_cube() :-
write('N'),write(ext),tab(1),
write(item),write(,),tab(1),
write(please),write(:).
output_format_cube(N,C) :-
write('C'),write(ube),tab(1),
write(of),tab(1),
write(N),tab(1),
write(is),tab(1),
write(C),write(.),nl.
/*
* Learn how to write this one!!
dosquare :-
repeat,
read(X),
( \+ number(X), !
;
Y is X*X,
write(Y)
% using "fail" here, do not need to wait true again.
).
*/
% repeat & read should be out of the parentheses
% others inside the parentheses
run_cube() :-
repeat,
input_format_cube,
read(N),
(\+ number(N), !
;
cube(N,C),
output_format_cube(N,C), fail).
% using writelist
bar(0) :- !.
bar(X) :-
write(*),
X1 is X-1,
bar(X1).
bars([]) :- !.
bars([H|T]) :-
bar(H),nl,
bars(T).
% what's this; consecutive number
showfile(N) :-
read(Term),
show(Term,N).
show(end_of_file,_) :- !.
show(Term,N) :-
write(N),tab(2),write(Term),nl,
N1 is N+1,
showfile(N1).
% ex 6.10
findterm(Term) :-
repeat,
read(Input),
% giving an ending
( Input == Term, !, fail
;
findterm(Term)).
% ch 6.7.4
% tests whether an atom X represents a taxi
taxi(X) :-
name(X,L),
L = [116,97,120,105|_].
% instantiates Sentence to Wordlist
getsentence(Wordlist) :-
read(Sentence),
sentence_to_list(Sentence,Wordlist).
sentence_to_list(Sentence,[Word|Wordlist]) :-
name(Sentence,Sentence1),
append(Word1,[32|Rest1],Sentence1),
name(Word,Word1),
name(Rest,Rest1),
sentence_to_list(Rest,Wordlist), !.
sentence_to_list(Sentence,[Word]) :-
name(Sentence,Sentence1),
append(Word1,[46|_],Sentence1),
name(Word,Word1).2.4 FAI: jugs(这是FAI这门课的一些Examples)
% the water jugs problem
% finish
% use a Num to constraint, makes a constraint-depth searching
action(jugs(GB,GS),[],jugs(GB,GS),_).
action(jugs(_,S),[fillBig|Remains],jugs(GB,GS),Num) :-
Num1 is Num - 1,
Num1 > 0,
action(jugs(4,S),Remains,jugs(GB,GS),Num1).
action(jugs(B,_),[fillSmall|Remains],jugs(GB,GS),Num) :-
Num1 is Num - 1,
Num1 > 0,
action(jugs(B,3),Remains,jugs(GB,GS),Num1).
action(jugs(_,S),[emptyBig|Remains],jugs(GB,GS),Num) :-
Num1 is Num - 1,
Num1 > 0,
action(jugs(0,S),Remains,jugs(GB,GS),Num1).
action(jugs(B,_),[emptySmall|Remains],jugs(GB,GS),Num) :-
Num1 is Num - 1,
Num1 > 0,
action(jugs(B,0),Remains,juges(GB,GS),Num1).
action(jugs(B,S),[fromBigToSmall|Remains],jugs(GB,GS),Num) :-
B + S =< 3,
S1 is B + S,
Num1 is Num - 1,
Num1 > 0,
action(jugs(0,S1),Remains,jugs(GB,GS),Num1)
;
B + S >= 3,
B1 is B-(3-S),
Num1 is Num - 1,
Num1 > 0,
action(jugs(B1,3),Remains,jugs(GB,GS),Num1).
action(jugs(B,S),[fromSmallToBig|Remains],jugs(GB,GS),Num) :-
B + S =< 4,
B1 is B + S,
Num1 is Num - 1,
Num1 > 0,
action(jugs(B1,0),Remains,jugs(GB,GS),Num1)
;
B + S >= 4,
S1 is S-(4-B),
Num1 is Num - 1,
Num1 > 0,
action(jugs(4,S1),Remains,jugs(GB,GS),Num1).
scheduleJugs(jugs(B,S),Schedule,jugs(GB,GS),Num) :-
action(jugs(B,S),Schedule,jugs(GB,GS),Num).2.5 FAI: cities
% cities
% facts
cityPath(boston,150,newyork).
cityPath(boston,3000,sanfrancisco).
cityPath(boston,1700,dallas).
cityPath(boston,1450,miami).
cityPath(newyork,150,boston).
cityPath(newyork,2900,sanfrancisco).
cityPath(newyork,1500,dallas).
cityPath(newyork,1200,miami).
cityPath(sanfrancisco,3000,boston).
cityPath(sanfrancisco,2900,newyork).
cityPath(sanfrancisco,1700,dallas).
cityPath(sanfrancisco,3300,miami).
cityPath(dallas,1700,boston).
cityPath(dallas,1500,newyork).
cityPath(dallas,1700,sanfrancisco).
cityPath(dallas,1600,miami).
findCityPath(E,[],E,_).
findCityPath(S,[cityPath(S,Mile,S1)|Remains],E,Num) :-
Num1 is Num - 1,
Num1 > 0,
cityPath(S,Mile,S1),
findCityPath(S1,Remains,E,Num1).
minimum_findCityPath(S,E,Output) :-
findall(Path,findCityPath(S,Path,E,10),AllPath),
minimumPath(S,AllPath,[Path|Paths]),
list_sort(Paths,Path,Output).
minimumPath(_,[],[]).
minimumPath(S,[H|T],[path([S|List],Sum)|Remains]) :-
cal_minimumPath(H,List,Formula),
Sum is Formula,
minimumPath(S,T,Remains).
cal_minimumPath([],[],0).
cal_minimumPath([cityPath(_,M,E)|Remains],[E|Path],Sum+M) :-
cal_minimumPath(Remains,Path,Sum).
list_sort([],Output,Output).
list_sort([path(P,S)|Remains],path(P1,S1),Output) :-
S =< S1,
list_sort(Remains,path(P,S),Output),!
;
list_sort(Remains,path(P1,S1),Output).2.6 FAI: blocks
% blocks
% fact
% needs to be changed, cannot be a fact, otherwise using the assertz and retrive
%on(c,a).
%on(a,table).
%on(b,table).
%move(on(A,B),move(A,B,C),on(A,C)) :-
% \+ on(_,A),
% \+ on(_,C).
%schdule(Plan) :-
% move().2.7 FAI: Blind Search - Depth search
% depth-first & breadth-first
% facts
edge(s,a,3).
edge(s,d,4).
edge(a,d,5).
edge(a,s,3).
edge(a,b,4).
edge(d,s,4).
edge(d,e,2).
edge(d,a,5).
edge(b,a,4).
edge(b,e,5).
edge(b,c,4).
edge(c,b,4).
edge(e,d,2).
edge(e,b,5).
edge(e,f,4).
edge(f,e,4).
edge(f,g,3).
edge(g,f,3).
schedule_depth_helper(_,_,_,0,_) :- !.
schedule_depth_helper(G,[G],G,_,0).
schedule_depth_helper(S,[S|Remains],G,Num,Cost+M) :-
Num1 is Num - 1,
Num1 > 0,
edge(S,S1,M),
schedule_depth(S1,Remains,G,Num1,Cost).
schedule_depth(S,Path,G,Num,Cost) :-
schedule_depth_helper(S,Path,G,Num,Formula),
Cost is Formula.
schedule_breath(S,Path,G,Num,Cost) :-
breadth_first(Path),
schedule_depth(S,Path,G,Num,Cost).
%% change depth-first to breadth-first
breadth_first([]).
breadth_first([_|L]) :-
breadth_first(L).2.8 FAI: Depth-first, Breadth-first, .. by list representation
% fact
% a
% | |
% b c
% | | | |
% d e f g
link(a,b).
link(a,c).
link(b,d).
link(b,e).
link(c,f).
link(c,g).
% depth-first searching
depth2.9 Unknown
% using helper and main :D
plus1_helper(zero,0).
plus1_helper(s(X),Num+1) :-
plus1(X,Num).
plus1(S,Num) :-
plus1_helper(S,Formula),
Num is Formula.% when ended
div(X,Y,D,R) :- div_helper(X,Y,D,R,zero).
div_helper(zero,_,zero,R,R).
div_helper(s(X),Y,D,R,T) :-
Y \== T,
div_helper(X,Y,D,R,s(T)).
div_helper(X,Y,s(D),R,Y) :-
div_helper(X,Y,D,R,zero).
% Boolean Formula
% unary predicates
eval(tru,tru).
eval(fal,fal).
eval(not(X),fal) :-
eval(X,tru).
eval(not(X),tru) :-
eval(X,fal).
% pair predicates
eval(and(X,Y),tru) :-
eval(X,tru),
eval(Y,tru).
eval(and(X,Y),fal) :-
eval(X,fal)
;
eval(Y,fal).
eval(or(X,Y),fal) :-
eval(X,fal),
eval(Y,fal).
eval(or(X,Y),tru) :-
eval(X,tru)
;
eval(Y,tru).% exercise 2
edge(a,b).
edge(b,a).
edge(b,d).
edge(d,b).
edge(c,d).
edge(d,c).
edge(b,c).
edge(c,b).
neighbor(X,Y) :- edge(X,Y).
path(X,Y) :-
neighbor(X,Y).
path(X,Y) :-
neighbor(X,Z), path(Z,Y).
path2(X,Y) :-
path2_helper(X,Y,[X]).
path2_helper(X,Y,T) :-
neighbor(X,Z),
\+ member(Z,T),
path2_helper(Z,Y,[Z|T]).
path2_helper(X,Y,T) :-
neighbor(X,Y),
\+ member(Y,T).% prime number
prime(1) :- !.
prime(N) :-
N1 is N-1,
prime_helper(N,N1), !.
prime_helper(_,1).
prime_helper(N,T) :-
N mod T =\= 0,
T1 is T - 1,
prime_helper(N,T1).
% prime_number list
all_primes(2,[2]) :- !.
all_primes(Max,[Max|L]) :-
prime(Max),
Max1 is Max - 1,
all_primes(Max1,L).
all_primes(Max,L) :-
\+ prime(Max),
Max1 is Max - 1,
all_primes(Max1,L).2.10 Chapter 9: Data Structures
% sorting list
% bubble sort
% Con: cannot deal with duplicated list √ fixed <- bubblesort using >, base case using >=
gt(X,Y) :- X > Y.
bubblesort(List,Solution) :-
append(List1,List2,List),
append([X,Y],List3,List2),
gt(X,Y),
% remembering using new variables to represent new List, Prolog's cons
append([Y,X],List3,List4),
% temperal solution 'Sorted' and final solution 'Solution'
append(List1,List4,Sorted),
bubblesort(Sorted,Solution), !.
bubblesort(Sorted,Sorted) :-
ordered(Sorted).
ordered([]) :- !.
ordered([_]) :- !.
ordered([H|T]) :-
ordered_helper(H,T), !.
ordered_helper(Min,[Max]) :- Max >= Min.
ordered_helper(Min,[Max|Tail]) :-
Max >= Min,
ordered_helper(Max,Tail).
% Answer
bubblesort_Ans(List,Sorted) :-
swap(List,List1), !,
bubblesort_Ans(List1,Sorted).
bubblesort_Ans(Sorted,Sorted).
swap([X,Y|Rest],[Y,X|Rest]) :-
gt(X,Y).
swap([Z|Rest],[Z|Rest1]) :-
swap(Rest,Rest1).
% insertion sort
insertionsort([],[]).
insertionsort([H|T],ST1) :-
insertionsort(T,ST),
insert_elem(H,ST,ST1).
insert_elem(X,[],[X]).
insert_elem(X,[Y|T],[X,Y|T]) :-
X =< Y.
insert_elem(X,[Y|T],[Y|T1]) :-
X > Y,
insert_elem(X,T,T1).
% quick sort
% do not forget the [] <-
quicksort([],[]).
quicksort([X|T],Sorted) :-
quicksort_split(X,T,Small,Big),
quicksort(Small,SmallSorted),
quicksort(Big,BigSorted),
append(SmallSorted,[X|BigSorted],Sorted).
quicksort_split(X,[Y|T],[Y|Small],Big) :-
X >= Y,
quicksort_split(X,T,Small,Big).
quicksort_split(X,[Y|T],Small,[Y|Big]) :-
X < Y,
quicksort_split(X,T,Small,Big).
quicksort_split(_,[],[],[]).% ex 9.1
merge1(L1,L2,L) :-
append(L1,L2,L3),
quicksort(L3,L).
% ex 9.4
div(L,L1,L2) :-
append(L1,L2,L),
length(L1,N1),
length(L2,N2),
abs(N1-N2) =< 1.
% mergesort(L,Sorted) :-
% div(L,L1,L2).% balanced tree
max(X,Y,X) :- X>Y, !.
max(_,Y,Y).
balanced(T) :-
balanced_helper(T,_).
balanced_helper(nil,0).
balanced_helper(t(L,_,R),H) :-
balanced_helper(L,LH),
balanced_helper(R,RH),
Diff is abs(LH-RH),
Diff =< 1,
max(LH,RH,H1),
H is H1 + 1.
add_tree(X,nil,t(nil,X,nil)).
add_tree(X,t(L,V,R),t(L1,V,R)) :-
add_tree(X,L,L1).
add_tree(X,t(L,V,R),t(L,V,R1)) :-
add_tree(X,R,R1).
add_to(T,X,T1) :-
add_tree(X,T,T1),
balanced(T1).calculate(Rabi,Chic,TotalFeet,TotalAnimal) :-
member(Rabi,[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]),
member(Chic,[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]),
TotalFeet is 4 * Rabi + 2 * Chic,
TotalAnimal is Rabi + Chic.% 虎眼石: Tiger 石英:White 孔雀石:Green 红宝石: Red
%
%2.11 FAI #2 lec 07
% FAI #2 Lec 07, example knapsack, without using the symmetric breaking
% e.g., initiate(Ks,Ms),run(Ks,Ms,Str).
initiate(
[kg(gr,12),kg(bl,2),kg(og,1),kg(ye,4),kg(gy,1)],
[dollar(gr,4),dollar(bl,2),dollar(og,1),dollar(ye,10),dollar(gy,2)]
).
% Condition
money(_,_,Weight,Money,List,Weight,Money,List) :- Money = 15, Weight =< 15.
% Main Recursive part
money(Kgs,Dols,Weight,Money,List,WO,MO,LO) :-
select(kg(Col,Kg),Kgs,Kgs1),
select(dollar(Col,Dol),Dols,Dols1),
Weight1 is Weight + Kg,
Money1 is Money + Dol,
money(Kgs1,Dols1,Weight1,Money1,[Col|List],WO,MO,LO).
% Find the best
bestOne([],[],[],best(W,M,C),best(W,M,C)).
bestOne([W|RWs],[M|RMs],[C|RCs],best(W1,M1,C1),Best) :-
M =< M1,
bestOne(RWs,RMs,RCs,best(W1,M1,C1),Best)
;
M > M1,
bestOne(RWs,RMs,RCs,best(W,M,C),Best).
% User interface
run(Ks,Ms,Best) :-
findall(Weights,money(Ks,Ms,0,0,[],Weights,Moneys,Colors),[W|RWs]),
findall(Moneys,money(Ks,Ms,0,0,[],Weights,Moneys,Colors),[M|RMs]),
findall(Colors,money(Ks,Ms,0,0,[],Weights,Moneys,Colors),[C|RCs]),
bestOne(RWs,RMs,RCs,best(W,M,C),Best).2.12 鸡兔同笼
% 鸡兔同笼,头共10,足共28
arrays(Arrays,Max) :-
arrays_helper(RArrays,Max),
reverse(RArrays,Arrays).
arrays_helper([],0).
arrays_helper([Head|Tail],Head) :-
Head1 is Head - 1,
arrays_helper(Tail,Head1).
run(C,R,H,F) :-
arrays(Hs,H),
member(C,Hs),
member(R,Hs),
H is C + R,
F is 2*C + 4*R,
!.2.13 FAI: Block World Domain STRIPS Planing
% FAI Block world STRIPS planning
%
% On(A,B)
% clear(A)
% schedule([clear(a),on(a,b),on(b,table),clear(c),on(c,d),on(d,e),on(e,table)],
% [clear(a),on(a,b),on(b,c),on(c,d),on(d,e),on(e,table)],
% Actions,
% 8).
schedule(Initial,Goal,Actions,Limit) :-
numOfOn(Initial,0,N),
addClearTableByN(Initial,Initial1,N),
schedule_helper(Initial1,Goal,Actions,Limit).
schedule_helper(_,_,[],0) :- !, fail.
schedule_helper(OnStates,Goal,[],_) :-
cleanClearTable(OnStates,OnStates1),
common_list(OnStates1,Goal),!.
schedule_helper(OnStates,Goal,[move(A,B)|Rest],N) :-
move(OnStates,A,B,OnStates1),
% cleanClearTable(OnStates1,OnStates2),
N1 is N - 1,
schedule_helper(OnStates1,Goal,Rest,N1).
common_list([X],[X]).
common_list(L1,L2) :-
select(X,L1,L11),
select(X,L2,L22),
common_list(L11,L22), !.
move(OnStates,A,B,OnStates1) :-
member(clear(A),OnStates),
member(clear(B),OnStates),
A \= B,
select(on(A,A_low),OnStates,OnStatesTemp),
select(clear(B),OnStatesTemp,OnStatesTemp1),
append([on(A,B),clear(A_low)],OnStatesTemp1,OnStates1).
cleanClearTable(OnStates,OnStates) :-
\+ member(clear(table),OnStates).
cleanClearTable(OnStates,Result) :-
select(clear(table),OnStates,OnStates1),
cleanClearTable(OnStates1,Result).
not_member(_,[]).
not_member(X,[X|_]) :- !, fail.
not_member(X,[_|Y]) :-
not_member(X,Y).
numOfOn(OnStates,N,N) :- \+ member(on(_,_),OnStates), !.
numOfOn(OnStates,N,Result) :-
select(on(_,_),OnStates,OnStates1),
N1 is N + 1,
numOfOn(OnStates1,N1,Result).
addClearTableByN(OnStates,OnStates,0) :- !.
addClearTableByN(OnStates,Output,N) :-
N1 is N - 1,
append([clear(table)],OnStates,OnStates1),
addClearTableByN(OnStates1,Output,N1).% test
test1(test1).
test2(test2).
% if - else
likes(X) :-
test1(X),!,fail
;
test2(X).
% test1/1 单纯没用了
likes2(X) :-
test1(X),fail, !
;
test2(X).Upadtes
于2021年7月14日1:37,完成对4.1-4.4的更新。
Acknowledgements
Reference from the book 《Prolog Programming for Artificial Intelligence: Fourth Edition》
Provided web system from SWISH: Sean's note for Prolog


